L'arbre de décision

Qu'est-ce qu'un arbre de décision ?

Un arbre de décision est un outil d'aide à la décision qui utilise une modélisation sous forme d'arbre pour projeter les décisions et leurs conséquences possibles. Cet outil prend également en considération les résultats d'événements aléatoires, les coûts des ressources.

Pourquoi utiliser un arbre de décision ?

Les arbres de décision sont très utile pour aider à identifier la stratégie la plus susceptible d'atteindre un objectif. Ainsi il permet à une personne d'évaluer différentes actions possibles en fonction de leur coût, leur probabilité et leurs bénéfices.

Structure de l'arbre de décision

Un arbre de décision a une structure semblable à un organigramme. Il est dessiné de gauche à droite. Un arbre de décision n'a que des nœuds de fractionnement mais pas de nœuds convergents. Par conséquent, utilisés manuellement, ils peuvent devenir très gros et sont souvent difficiles à dessiner entièrement à la main.

Le nœud le plus à gauche dans un l'arbre de décision est appelé le nœud racine d'où découlent plusieurs résultats possibles. Chacun de ces résultats mène à d'autres nœuds, d'où émanent d'autres possibilités.  Une et une seule de ces alternatives peut être sélectionnées.

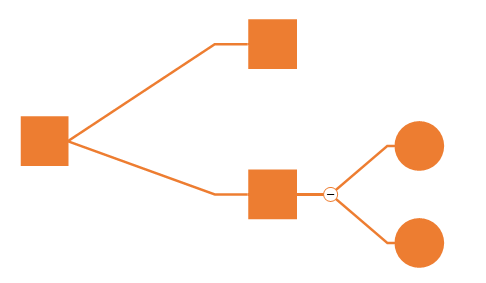
Un arbre de décision se compose de trois types de nœuds:

• Noeuds de décision - généralement représentés par des carrés
• Nœuds aléatoire - généralement représentés par des cercles
• Noeuds d'extrémité ou noeud terminal - généralement représentés par des triangles.  L'extrémité droite de chaque chemin dans l'arborescence est appelée point d'extrémité, et chaque le point final représente le résultat final de suivre un chemin depuis la racine nœud de l'arbre de décision à ce point final.
• Les branches émanant à droite à partir d'un nœud de décision représentent l'ensemble des alternatives de décision qui sont disponibles.
• Le nombre affiché entre parenthèses sur chaque branche d'un nœud aléatoire est la probabilité que le résultat indiqué sur cette branche se produira au nœud de hasard.

Si, dans la pratique, les décisions doivent être prises en ligne sans rappel en raison de connaissances incomplètes, un arbre de décision doit être mis en parallèle par un modèle de probabilité comme modèle de meilleur choix ou algorithme de modèle de sélection en ligne. Une autre utilisation des arbres de décision est comme moyen descriptif pour calculer les probabilités conditionnelles. Les arbres de décision, les diagrammes d'influence, les fonctions d'utilité et d'autres outils et méthodes d'analyse des décisions sont enseignés aux étudiants de premier cycle dans les écoles de commerce, d'économie de la santé et de santé publique, et sont des exemples de méthodes de recherche opérationnelle ou de sciences de la gestion.

Construction de l'arbre de décision

Les différentes décisions possibles sont situées aux extrémités des branches (les « feuilles » de l'arbre), et sont atteintes en fonction de décisions prises à chaque étape. Pour lire une classification d'un objet de données individuel, on descend du nœud racine le long de l'arborescence. Un attribut est interrogé pour chaque nœud et une décision est prise concernant la sélection du nœud suivant. Cette procédure se poursuit jusqu'à ce que vous atteigniez une feuille. La feuille correspond à la classification.

Arbre de décision et machine learning

L'apprentissage par arbre de décision est l'une des approches de modélisation prédictive utilisées dans les statistiques, l'exploration de données et l'apprentissage automatique. Il utilise un arbre de décision (comme modèle prédictif) pour passer des observations sur un élément (représenté dans les branches) aux conclusions sur la valeur cible de l'élément (représentée dans les feuilles).

Exemple d'arbre de décision

Présentation de l'exemple

Soit un club de 10000 membres. Chaque membre paie une souscription de 800 euros par année. Le coût par membre restera au même niveau à 100 euros. Afin de péreniser sa clientèle, le club doit décier ou non d'investir dans de nouveaux équipement.

Deux options apparaissent :

Option 1 : Aucun investissement. Dans cette situation, le nombre de membre va décroitre et descendre à 6000 membres. Le coût par membre restera au même niveau à 100 euros.

Option 2 : le club investi 400 000 euros. L'effet sur le nombre de membre est le suivant :

• Probalité de 0.4  que le nombre de membre se maintienne à 10 000.
• Probabilité de 0.6 que le nombre de membre atteingne 11 000 membres.

Effet sur les coûts de fonctionnement par membre.

• Probabilité de 0.5 que les coûts augmentent à 120 euros par an
• Probabilité de 0.5 que les coûts augmentent à 140 euros par an

Les étapes de construction de l'arbre de décision

Modélistion de l'option 1

Si le gérant décide de ne rien faire, le gain sera de 7 000 000. Pour ce calcule on retire es 800 euros de cotisation les 100 euros de frais de fonctionnement et nous mutiplions le résultat par le nombre d'adhérents.

Modélistion de l'option 2

Nous représentons dans un premier temps le noeud aléatoire du nombre d'adhérent qui peut être soit de 10 000 ou de 11 000.

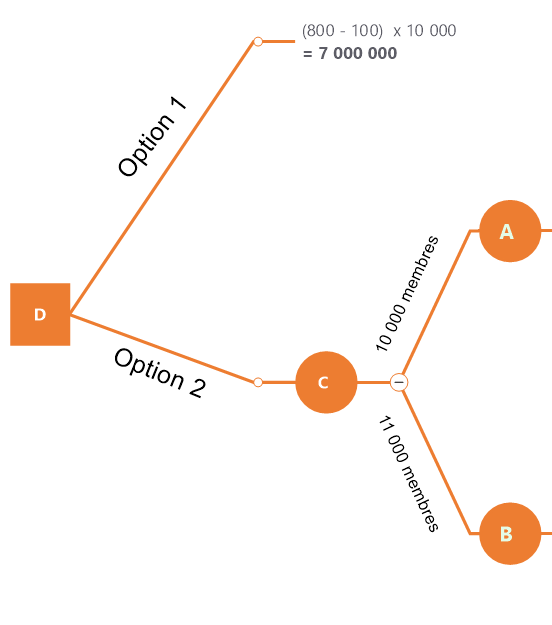
Nous opérons ensuite une seconde séparation avec les différents frais de fonctionnement pour chacune des branches

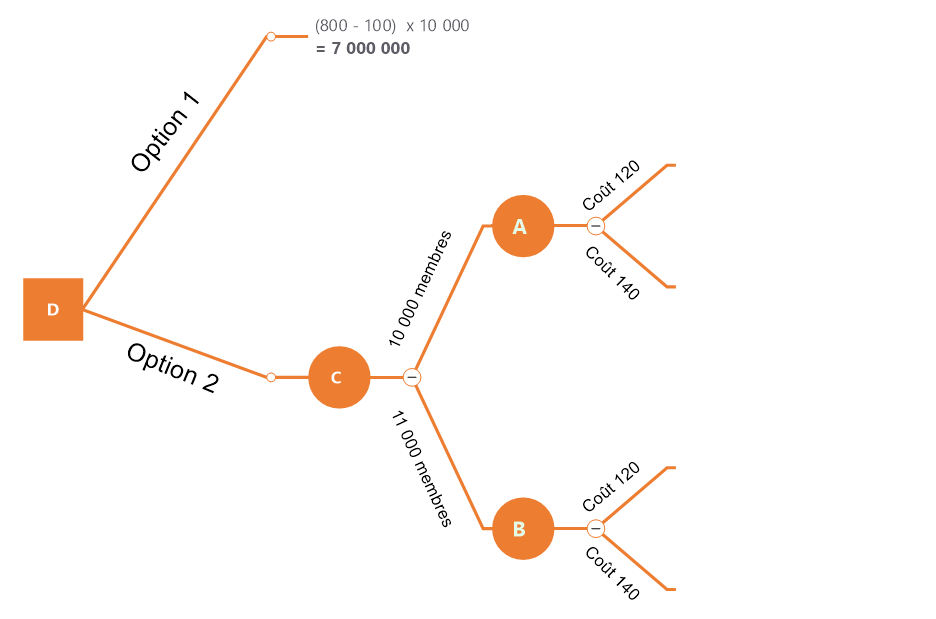
Réalisation des calculs de l'option 2

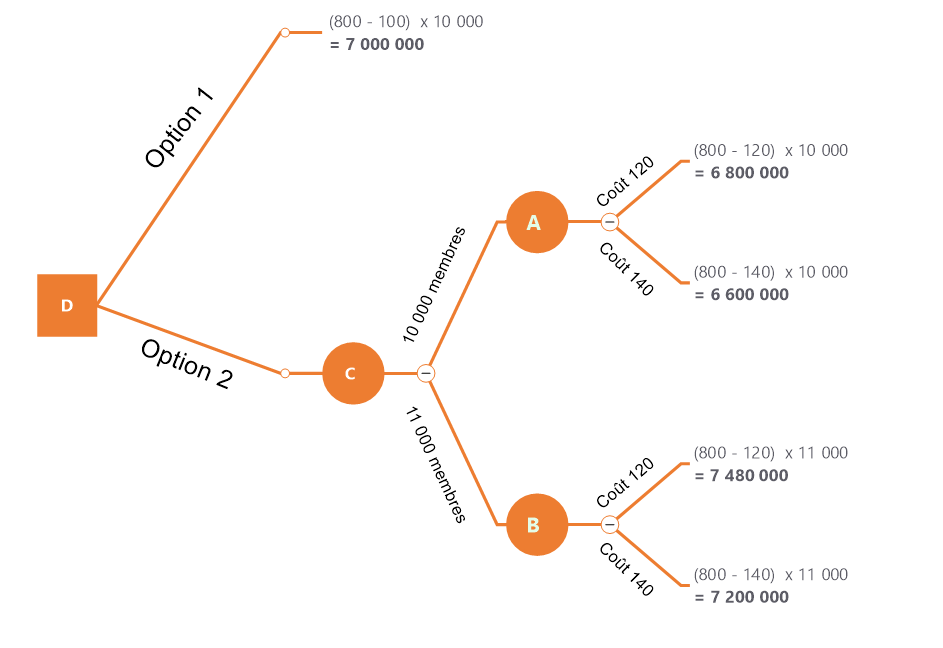
Ajout des probabilités

Nous ajoutons les probabilités associées à chaque branche. Vous noterez également que les noeuds sont identifié par une lettre qui permettra de les identifier pour le calcul qui suit.

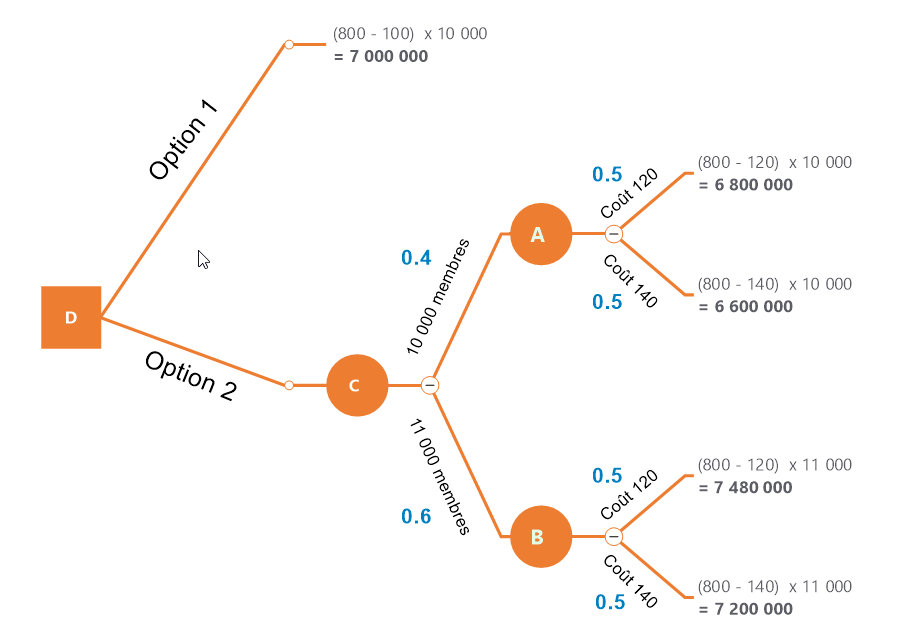
Synthèse des options

Valeur espérée	Calcul	Résultat
Val A	6 800 000 x 0.5 + 6 600 000 x 0.5	6 700 000
Val B	7 480 000 x 0.5 + 7 200 000 x 0.5	7 340 000
Val C	6 700 000 x 0.4 + 7 340 000 x 0.6	7 084 000

La valeur C correspond au gain espéré de l'option n°2. Ce gain est supérieur au gain espéré de l'otion 1. Donc nous choisissons l'option 2.